Lattice paths
2014-09-11
Problem 015: Lattice paths
Starting in the top left corner of a 2×2 grid, and only being able to move to the right and down, there are exactly 6 routes to the bottom right corner.
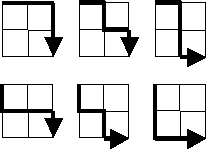
How many such routes are there through a 20×20 grid?
Solution:
v
000000000000000000000
000000000000000000000
000000000000000000000
000000000000000000000
000000000000000000000
000000000000000000000
000000000000000000000
000000000000000000000
000000000000000000000
000000000000000000000
000000000000000000000
000000000000000000000
000000000000000000000
000000000000000000000
000000000000000000000
000000000000000000000
000000000000000000000
000000000000000000000
000000000000000000000
000000000000000000000
000000000000000000000 > v
>v >00g1-10gg00g10g1-g+00g10gpv
>100p110p> 00g492*+10g-*|>00g392*+`#^_>00g1-10g1-*| vp01+1g01p00-1g00<
^p011p00+g01g00< >100g10gp ^
|! `+2*58+g00g01 <
@.g:*73<
000000000000000000000
000000000000000000000
000000000000000000000
000000000000000000000
000000000000000000000
000000000000000000000
000000000000000000000
000000000000000000000
000000000000000000000
000000000000000000000
000000000000000000000
000000000000000000000
000000000000000000000
000000000000000000000
000000000000000000000
000000000000000000000
000000000000000000000
000000000000000000000
000000000000000000000
000000000000000000000
000000000000000000000 > v
>v >00g1-10gg00g10g1-g+00g10gpv
>100p110p> 00g492*+10g-*|>00g392*+`#^_>00g1-10g1-*| vp01+1g01p00-1g00<
^p011p00+g01g00< >100g10gp ^
|! `+2*58+g00g01 <
@.g:*73<
Start
??
Pause
Reset
Output:
Stack: (0)
Explanation:
We create a 21x21 grid of the edges in our graph, then we set the value on each edge to the number of possible paths to (0|0).
For the top-left edge this is 1. For the edges in the first row/column it is also 1. For every other edge it is the above edge + the left edge.
And in the end we are only interested in the value of the bottom-right edge - this value is our result.
| Interpreter steps: | 61 202 |
| Execution time (BefunExec): | 47ms (1.30 MHz) |
| Program size: | 78 x 27 |
| Solution: | 137846528820 |
| Solved at: | 2014-09-11 |

